
Some flavors have fewer than the expected 200 pieces and some have more. Without doing any statistics, we can see that the number of pieces for each flavor are not the same. This is more than the requirement of five expected values in each category.īased on the answers above, yes, the Chi-square goodness of fit test is an appropriate method to evaluate the distribution of the flavors in bags of candy. For 10 bags in our sample, we expect 10 x 20 = 200 pieces of candy in each flavor. This means we expect 100 / 5 = 20 pieces of candy in each flavor from each bag. We expect to have equal numbers for each flavor. We have the count of each flavor in 10 bags of candy. Our categorical variable is the flavors of candy.We have a simple random sample of 10 bags of candy.Let’s start by answering: Is the Chi-square goodness of fit test an appropriate method to evaluate the distribution of flavors in bags of candy? Our hypothesis is that the proportions of the five flavors in each bag are the same. Let’s use the bags of candy as an example. We collect a random sample of ten bags. Each bag has 100 pieces of candy and five flavors. A data set that is large enough so that at least five values are expected in each of the observed data categories.The Chi-square goodness of fit test is not appropriate for continuous data.
#CHI SQUARE TEST MINITAB FULL#
Data values that are a simple random sample from the full population.To apply the goodness of fit test to a data set we need: The idea we'd like to test is that each team has the same proportion of children with a lot, some or no experience as the league as a whole. Suppose we know that 20 percent of the players in the league have a lot of experience, 65 percent have some experience and 15 percent are new players with no experience. For a group of children’s sports teams, we want children with a lot of experience, some experience and no experience shared evenly across the teams.The idea we'd like to test is that the proportions of the five flavors in each bag are the same. The bags should contain an equal number of pieces of each flavor. We have bags of candy with five flavors in each bag.We also need an idea, or hypothesis, about how that variable is distributed.

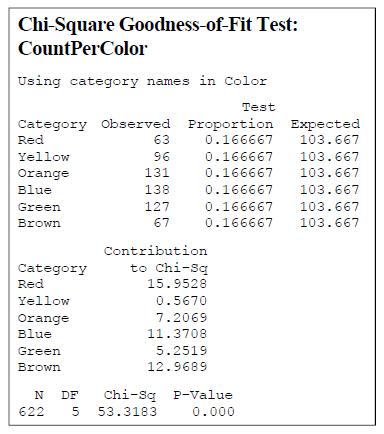

The table above has been entered in columns 4 to 7 of the Minitab file.State the null and alternative hypotheses. Before conducting the test, determine the percentage in each group that supports same sex marriage.Conduct a hypothesis test to determine if Americans’ opinions about same‐sex marriage are age related? The data is summarized in the two‐way table shown below. Pew Research conducted a poll of 2000 American adults asking whether they Favor or Oppose same‐sex marriage.Do you reject or fail to reject \(H_o\)? Then state your conclusion in the context of the problem.Conduct the test at a significance level of 5%, using MINITAB command: Stat>Table > Chi Square Goodness of Fit. Set the Observed Counts to the column you just entered and choose Equal Proportions. The data is in the first 2 columns of the Mintab worksheet.


 0 kommentar(er)
0 kommentar(er)
